√100以上 1^2 2^2 3^2 .... n^2 = n(n 1)(2n 1)/6 161205

Nov 24, 16 · How do I use summation notation to write the series 22 66?51 Pull out like factors 2n 2 2 = 2 • (n 2 1) Polynomial Roots Calculator 52 Find roots (zeroes) of F(n) = n 2 1 Polynomial Roots Calculator is a set of methods aimed at finding values of n for which F(n)=0 Rational Roots Test is one of the above mentioned toolsHow to show that the sequence 2 n 2 Plug in 1 3 for n a 1 3 = 2 8 6 1 1 1

Vollstandige Induktion 2n 3 3n 2 N Sei Durch 6 Teilbar Mathelounge

1^2 2^2 3^2 .... n^2 = n(n 1)(2n 1)/6

1^2 2^2 3^2 .... n^2 = n(n 1)(2n 1)/6-Statement P (n) is defined by 1 2 2 2 3 2 n 2 = n (n 1) (2n 1)/ 2 STEP 1 We first show that p (1) is true Left Side = 1 2 = 1 Right Side = 1 (1 1) (2*1 1)/ view the full answerSimple and best practice solution for 2/3(1n)=1/2n equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so

How To Prove That Math Frac 2 N 2 N 1 2 N 1 2 N 3 2 Quora

O(2^(n1)) is the same as O(2 * 2^n), and you can always pull out constant factors, so it is the same as O(2^n) However, constant factors are the only thing you can pull out 2^(2n) can be expressed as (2^n)(2^n), and 2^n isn't a constant So, the answer to your questions are yes and noSubmit your answer Related Questions in Mathematics Asked By adminstaff @ 25/09/19 0936 PM Mathematics 1 Answers Let X=the amount of water in the bucket A bucket holds 2 2/3 gallons of water The bucket is 5/6 full How much water is in the bucketAnswer to Prove that 1^2 2^2 3^2 n^2 = n(n 1)(2n 1)/6 for n greaterthanorequalto 1 Prove that 1^2 3^2 5^2

MAT V1102 – 004 Solutions page 2 of 7 8 Since ex is a strictly increasing function, e1/n ≤ e for all n ≥ 1 Hence, we have e1/n n3/2 ≤ e n3/2 Since P en−3/2 converges (it's a pseries with p = 3/2 > 1), the comparison test implies that P e1/nn−3/2 also converges 9 If f(n) = (n2)(n3) (n1)3 then f′(n) = (2n5)(n1)3 − 3(n2 5n6)(n1)2 (n1)6 = − n2 8n13$3(1^22^2n^2)3(123n)1n=(n1)^3,$ từ đó ta có công thức cần cm Bài viết đã được chỉnh sửa nội dung bởi halloffame 2251 hoctrocuanewton yêu thíchLet S(x) be the partial sum of a GP in the form

Simple and best practice solution for 1/2(2n6)=5n12n equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkMar 01, 18 · Find the sum up to n terms of the series 123 234 n(n1)(n2) In this 123 represent the first term and 234 represent the second term Examples Input 2 Output 30 123 234 = 6 24 = 30 Input 3 Output 90Oct 07, 19 · Find the sum up to n terms of the series 123 234 n(n1)(n2) In this 123 represent the first term and 234 represent the second term Let's see an example to understand the concept better, Input n = 5 Output 4 Explanation 123 234 345 456 567 = 6 24 60 1 210 = 4 nth term = n(n1)(n2

1 2 3 2 5 2 2n 1 2 N 4n 2 1 3 Với N Thuộc N Toan Học Lớp 11 Bai Tập Toan Học Lớp 11 Giải Bai Tập Toan Học Lớp 11 Lazi Vn Cộng đồng Tri Thức Giao Dục

Solved Exercises 1 3 1 Use Mathematical Induction To Pro Chegg Com

Click here 👆 to get an answer to your question ️ Problem 2 Prove that 1 2 2 2 3 2 n 2 = n (n 1) (2n 1)/ 6 For all positive integers n komali000 komali000In how many ways 10 different books taken 4 at a time can be arranged in an almirah such that a particular book 1is always taken 2is never taken a person has 36 banana sampling 144 apple sampling 234 orange sampling hw wants to plant them in saparete rows but wants to ensure that minimum space utilized so what is the number of minimum rows heThe sum $1^2 2^2 3^2 4^2 \\cdots n^2 = \\frac{n(n1)(2n1)}{6}$ What is the value of $21^2 22^2 \\cdots 40^2$?

Fm Series Ppt Download

Aufgabensammlung Zur Vollstandigen Induktion

Aug 15, 09 · 1^22^23^2n^2 We know that (x1)^3x ^3= 3x^23x1 Putting x=1,2n, we get 2^31^3=3(1)^23(1)1 3^32^3=3(2)^23(2)1 (n1)^3n^3=3(n)^23(n)1Learn with Tiger how to do 2/3(1n)=1/2n fractions in a clear and easy way Equivalent Fractions,Least Common Denominator, Reducing (Simplifying) Fractions Tiger Algebra SolverOct 03, 08 · In this case A(n) = 2^2n 1 Assume A(n) is div by 3 Ie 3 2^2n 1 Prove A(n1) if div by 3 Ie 3 2^2(n1) 1 Show that A(n1) A(n) is divisible by 3 2^2(n1) 1 (2^2n 1) = 2^2n2 2^2n = 2^2n(2^2 1) = 2^2n(3) That's it

Binomial Theorem 169 On Is Even The Middle Term Of The Expansion 1 X Is Solution As 2n Is E 1 Term Which Is Given By Ie N 1

Find The Sum Of The Following Series Up To N Terms 1 3 1 1 3 2 3 1 3 1 3 2 3 3 3 1 3 5 Mathematics Shaalaa Com

The sum of the first n squares, 1 2 2 2 n 2 = n(n1)(2n1)/6 For example, 1 2 2 2 10 2 =10×11×21/6=385 This result is usually proved by a method known as mathematical induction, and whereas it is a useful method for showing that a formula is true, it does not offer any insight into where the formula comes fromJun 06, 17 · How do we find the sum of the series up to n terms of S(n) = 1 2/2 3/2^2 4/2^3 n/2^(n – 1) ?Solve for n 1/2n 3/4n = 1/2 LOGIN TO VIEW ANSWER Do you know the better answer!

Quiz 7 The Way I Expected It How To Do It 1 Let P N Be The Statement That N 2 N N 1 2n 1 6 For The Positive Integer N Be Ppt Download

Vollstandige Induktion 2n 3 3n 2 N Sei Durch 6 Teilbar Mathelounge

Feb 15,  · Transcript Ex 41,8 Prove the following by using the principle of mathematical induction for all n ∈ N 12 222 323 n2n = (n – 1) 2n1 2 Let P(n) 12 222 323 n2n = (n – 1) 2n1 2 For n = 1, LHS = 12 = 2 RHS = (1 – 1) 211 2 = 0 2 = 2, Hence, LHS = RHS ∴ P(n) is true for n = 1 Assume P(k) is true 12 222 323 k2k = (kProve 1 Show that is true for and 2 Assume is true for some positive integer , then show theSep 05, 13 · The relation 2462n = n^2n has to be proved If n = 1, the right hand side is equal to 2*1 = 2 and the left hand side is equal to 1^1 1 = 1 1 =

Find The Sum To N Terms Of The Series 1 2 3 2 3 4 3 4 5 Mathematics Shaalaa Com

Cormen Gate Overflow

Solve for n 21/2n=3n16 Combine and Move all terms containing to the left side of the equation Tap for more steps Subtract from both sides of the equation Simplify the left side of the equation Tap for more steps To write as a fraction with a common denominator, multiply byA _ { n } = \frac { 4 n ^ { 2 } } { ( 2 n 1 ) ( 2 n 1 ) } a n Get Started Similar Problems from Web Search How to show that the sequence \frac{n^2n1}{2n^24n1} converges to \frac{1}{2} by the \epsilonN definition?The problem is that your nth term is incorrect \frac{2n1}{2n} \frac{2n2}{2n1} Will get you (3/2 4/3) for n=1, (5/4 6/5) for n=2 and so on Simplifying, this makes the nth term The problem is that your nth term is incorrect

Solved Prove Each Of The Following Statements Using Mathematical Induction 3 12 22 32 N2 1 2 1 6 Forallnzl B I 1 2 2 3 N Course Hero

Reihen Endliche Schreibweise Und Beweis Durch Induktion 2 4 6 8 10 2n N 1 N Mathelounge

Click here👆to get an answer to your question ️ 1n 2(n 1) 3(n 2) (n 1)2 n1 =(1) we will prove that the statement must be true for n = k 1May 13, 15 · Using Mathematical Induction, prove the following a) 6^n 1 is divisible by 5, for n>_0 maths prove by mathematical induction that 7n4n1 is divisible by 6 algebra Prove by mathematical induction that x^2n y^2n has a factor of xy

Ncert Exemplar Class 11 Maths Chapter 9 Sequence And Series Learn Cbse

Solved In 1 6 Prove The Following Statements By Mathemat Chegg Com

Thanks you all for trying to help DDTHAI That is the correct formula ItI have wondered how the closed form for the sum of squares for the first n natural numbers was derived Given the formula for the sum 1^22^2n^2= n(n1)(2n1)/6 I learned to prove its correctness using mathematical induction However, I neverMay 12, 19 · Chứng minh \{1^2} {2^2} {n^2} = \frac{{n(n 1)(2n 1)}}{6}\ Đây là một bài toán rất thường gặp trong chương trình toán học Bài toán mang tầm tư duy cao

A N Excerpt From The Chapter Sequence In The Textbook 4 Download Scientific Diagram

Show That N N 1 2n 1 Is Divisible By 6 So That The Formula

Trong sách bài tập 11 toán giải tích (bài 472) có ghi 1^2 2^2 n^2 = n(n1)(2n1)/6 mình không hiểu lí do tại sao mong mọi người giúp!In Exercises 115 use mathematical induction to establish the formula for n 1 1 12 22 32 n2 = n(n 1)(2n 1) 6 Proof For n = 1, the statement reduces to 12 = 1 2 3 6 and is obviously true Assuming the statement is true for n = k 12 22 32 k2 = k(k 1)(2k 1) 6;Can be used to divide mixed numbers 1 2/3 4 3/8 or can be used for write complex fractions ie 1/2 1/3 An asterisk * or × is the symbol for multiplication Plus is addition, minus sign is subtraction and () is mathematical parentheses

Prove That 1 2 2 2 3 2 N 2 N N 1 2n 1 6

Sum Of N Terms Of The Series 2n 1 2 2n 3 3 2n 5 Is

How do you derive that for the series that S(n)=(n(n1)(2n1))/6 Hi Shamus, The simplest method is mathematical induction Let P(n) be the the conjectured identity Check its validity for n=1 Assume that you have checked it out all the way for n = 1, 2, , k1 Now use that assumption to show the validity for n = k1^2 2^2 3^2 n^2 = n(n1)(2n1)/6 for all positive integral values of n Answer by solver() (Show Source) You can put this solution on YOUR website!Using induction, how can I solve this problem?

Lim N Oo 1 2n 1 1 2n 2 1 2n N I N 1 3 B I N

ลำด บและอน กรม

For the proof, we will count the number of dots in T(n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division!Try to make pairs of numbers from the set The first the last;Dec 07,  · Example 1 For all n ≥ 1, prove that 12 22 32 42 n2 = (n(n1)(2n1))/6 Let P (n) 12 22 32 42 n2 = (n(n1)(2n1))/6 For n = 1, LHS = 12

Natural Numbers Series 23 4 Sideway Output To

Ex 4 1 7 Prove 1 3 3 5 5 7 2n 1 2n 1 Class 11

What is the difference between a sequence and a series in math?Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeSolve for n 32(n4)>1 Simplify Tap for more steps Simplify each term Tap for more steps Apply the distributive property Multiply by Add and Move all terms not containing to the right side of the inequality Tap for more steps Subtract from both sides of the inequality

Sideway Bick Blog On 21 05 From Sideway To

Prove That 2n 1 N 2 N1 3 5 2n 1 2n 1

We now have the relation true for n = 1 and if the relation is true for any n greater than 1, it it also true for n 1 This proves that for all values of n 1^2 2^2 3^2 n^2 = 1/6 n(n1Sep 14, 10 · 1^2 2^2 3^2 2^n = 2^(n1) Sum n^2 = ( n / 6 )( n 1 )( 2n 1 ) That would be right for all n's that I have tried so far!Proof As with any infinite series, the sum is defined to mean the limit of the partial sum of the first n terms = as n approaches infinity By various arguments, one can show that this finite sum is equal to = As n approaches infinity, the term approaches 0 and so s n tends to 1 History Zeno's paradox This series was used as a representation of many of Zeno's paradoxes

Python Program To Calculate Sum Of Series 1 2 3 N

ลำด บและอน กรม

How do I use summation notation to write the series 22 66 11?To do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T(4)=1234 =Aug 08, 18 · An efficient approach is to find the 2^(n1) and subtract 1 from it since we know that 2^n can be written as 2 n = ( 2 0 2 1 2 2 2 3 2 4 2 n1) 1 Below is the implementation of above approach

Principle Of Mathematical Induction Class Xi Exercise 4 1 Part 1 Breath Math

Math 1210 Solutions To Assignment 1 Fall 12 1 A Use

Let p(n)=1 2 2 2 3 2 n 2 = n(n1)(2n1)/ 6 For n = 1, the statement reduces to 1 2 =1 · 2 · 3/6 and is obviously true Assuming the statement is true for n = kBut how do prove that the formula is right?The second the one before last It means n1 1;

Metodo De Induccion 1 2 2 2 3 2 N 2 N N 1 2n 1 6 Youtube

Ex 4 1 6 1 2 2 3 3 4 N N 1 N N 1 N 2 3

N2 2 The result is always n And since you are adding two numbers together, there are only (n1)/2 pairs that can be made from (n1) numbers So it is like (N1)/2 * NSuppose s 1 2 3 n term also s n n 1 n 2 3 2 1 adding that 2s n 1 n 1 n 1 n 1 n 1 n 1 n 1 2s Answer added by Md Mozaffor Hussain Mozaffor, Assistant Teacher , BIAM Model school and collegeThe Basel problem is a problem in mathematical analysis with relevance to number theory, first posed by Pietro Mengoli in 1650 and solved by Leonhard Euler in 1734, and read on 5 December 1735 in The Saint Petersburg Academy of Sciences Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was

Prove By Induction That 1 2 2 2 3 2 N 2 Youtube

Math 3210 3 Hw 7 The Natural Numbers And Induction

Jun 27, 17 · #"using the method of "color(blue)"proof by induction"# #"this involves the following steps "# #• " prove true for some value, say n = 1"# #• " assume the result is true for n = k"#Free equations calculator solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps Type in any equation to get the solution, steps and graph

Pdf Important Sum Formulas Omid Motahed Academia Edu

6 1 3 Areas As Limits Of Riemann Sums

By Pmi Prove N N 1 2n 1 Is Divisible By 6 Maths Principle Of Mathematical Induction Meritnation Com

Sum Of N N Or N Brilliant Math Science Wiki

How Can One Prove That Math 1 2 Dots N 2 1 3 2 3 Dots N 3 Math Without Using Mathematical Induction Quora

Is This Modern Programming Interview Challenge S Solution Unreliable Stack Overflow

Tinh Cac Giới Hạn Lim 3n 2 N 1 N 3 4n 2 6 Toan Học Lớp 11 Bai Tập Toan Học Lớp 11 Giải Bai Tập Toan Học

Solution3

Q Prove That 1 3 2 4 3 5 N N 2 1 6n N 1 2n 7 V Nen Maths Principle Of Mathematical Induction Meritnation Com

Catalan Number Wikipedia

Rd Sharma Solutions For Class 11 Chapter 12 Mathematical Induction Download Free Pdf

1 3 2 4 3 5 N N 2 N N 1 2n 7 6

Prove By Mathematical Induction 1 2 2 2 3 2 N 2 N N 1 2n 1 6 N N Sarthaks Econnect Largest Online Education Community

Wallis Product Wikipedia

Vollstandige Induktion Summe Von Quadratzahlen N N 1 2n 1 6 Mathelounge

Strategy For Testing Series Solutions

Solved Prove The Following Using Mathematical Induction Chegg Com

Prove By Induction 1 2 2 2 3 2 4 2 N 2 N N 1 2n 1 6

How To Prove That Math Frac 2 N 2 N 1 2 N 1 2 N 3 2 Quora

Sideway Bick Blog On 18 05 From Sideway To

Ncert Solutions For Class 9 10 11 And 12 Prove The Following By Using The Principle Of Mathematical Induction For All N N

Determining N In A Given Sequence Frac 1 3 5 2n 1 2 4 6 2n Frac 11 12 Mathematics Stack Exchange

If Sn 1 3 6 10 N N 1 2 Then Sn Is Brainly In

Notes On Topics Of Algebra Notes

Solved Complete Following Questions Question 19 Complete Part D 1 Show N 0 1 2 Following True 12 Q

Solved Use Mathematical Induction To Prove That N N 1 2n Chegg Com

Powers Of Natural Numbers Series 26 4 Sideway Output To

Sum Of Arithmetic Sequence Calculator

Prove By Induction 1 2 2 2 3 2 4 2 N 2 N N 1 2n 1 6

Solved 5 Prove 12 32 52 2n 1 2 N 1 2n 1 2n 3 3 Whenever N Nonnegative Integer 6 Prove 111 22 N Q

Why Does N N 1 2n 1 6 N 1 2 N 1 N 2n 1 6 N 1 Mathematics Stack Exchange

A N Excerpt From The Chapter Sequence In The Textbook 4 Download Scientific Diagram

1 1 2 3 2 2n 1 2n 1 2n 1 N 3 Proof By Mathematical Induction 2 1 2 2 2 2 3 2 N 1 2 N 1 Proof By Mathematical Induction Mathematics Topperlearning Com Phd6kncc

n2 Formula

Prove By The Method Of Induction For All N Belongs To N 1 2 2 2 3 2 N 2 N N 1 2n 1 6 Brainly In

How To Prove Using Induction That 12 Divides 2 2n 2 3n 4 3n 2 4 Quora

Find The Sum To N Terms Of The Series 1 2 3 2 3 4 3 4 5 Sarthaks Econnect Largest Online Education Community

By Mathematical Induction Prove That 1 2 3 N N N 1 2n 1 6 Brainly In

Solved Prove That 1 2 2 2 3 2 N 2 N N 1 2 Chegg Com

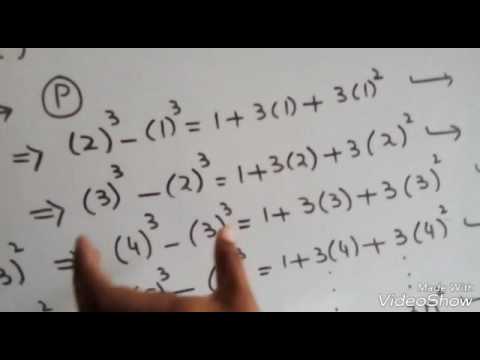
Prove That 1 2 2 2 3 2 N 2 N N 1 2n 1 6 Youtube

求證1 2 3 N N N 1 2n 1 6的詳細過程 台部落

Wallis Product Wikipedia

A Scientist Gave A Lecture On Astronomy He

Lim N N 1 N 2 3n N 2n 1 N Is Equal To Sarthaks Econnect Largest Online Education Community

3 Mathematical Induction Pdf Free Download

N Grosser 2 Hoch N 1 Mal N 2 Zum Quadrat Youtube

Serieshw 2

Answered I Proving A Formula Use Mathematical Bartleby

Answered Define The Double Factorial Of N Bartleby

n2 Formula Proof

Basel Problem Wikipedia

Cs 2 Discrete Structures And Their Applications Mathematical

An Introduction To Mathematical Induction The Sum Of The First N Natural Numbers Squares And Cubes Math Wiki

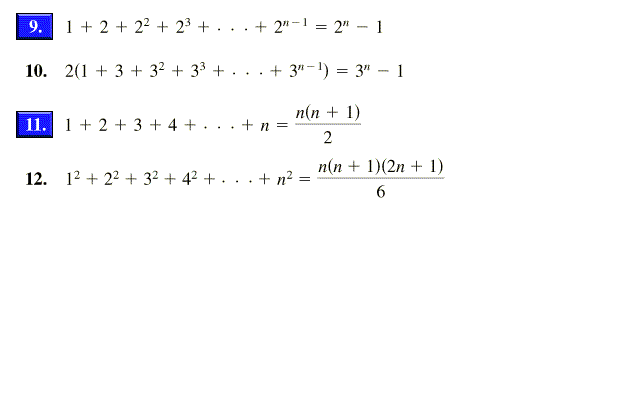
Solved In Exercises 5 18 Use Mathematical Induction To P Chegg Com

What Is The Sum Of The Series 3 6 4 7 5 8 Up To N 2 Terms Quora

Ex 4 1 5 Prove 1 3 2 32 3 33 N 3n 2n 1 3n 1

Mathematical Induction Doc

Ism Et Chapter 8

Prove Using Mathematical Induction That 2 3n 3 N Is Divisible By 5 For All N 1 Mathematics Stack Exchange